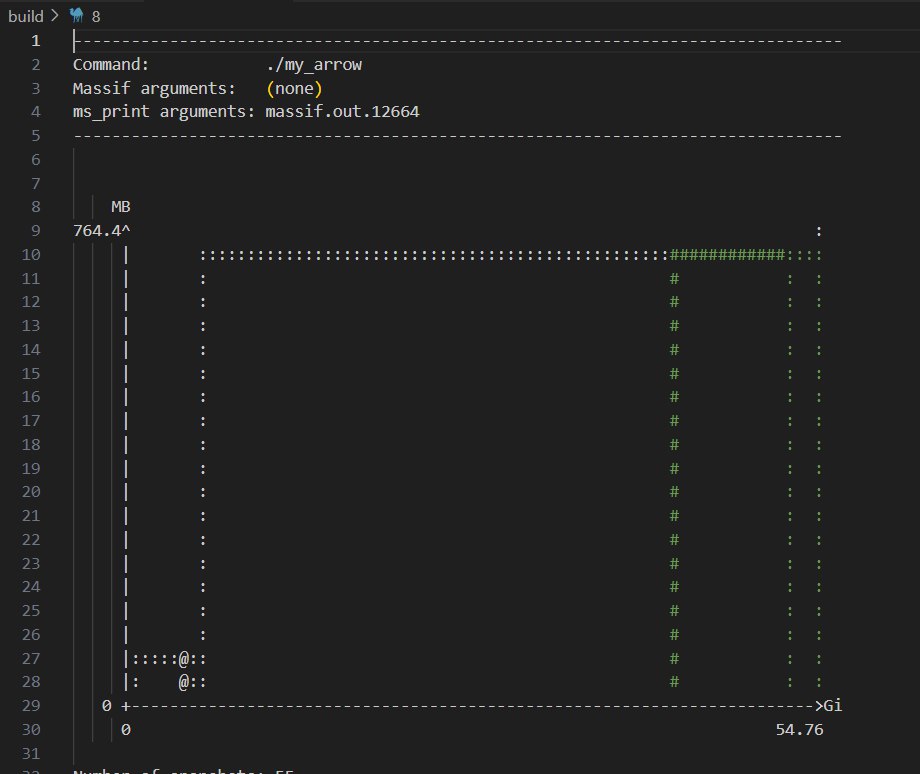
The code is looking for a min value of an array of doubles of 100M size.
The result is arrow::compute::MinMax is 3-4 times faster than std::minmax_element without noticeable memory overhead.


Programmer in Canada
The code is looking for a min value of an array of doubles of 100M size.
The result is arrow::compute::MinMax is 3-4 times faster than std::minmax_element without noticeable memory overhead.


Our online Coding Dojo sessions became the most powerful learning experience for me, and recently we came across Conway’s Game of Life.
I remember playing this game on paper when I was a child. Yesterday I had the pleasure to code the rules and see them working.
To make it more fun, we in our Coding Dojo club decided to separate concerns between “cells” and “grid” where the cells exist. After an exciting discussion for which I am grateful to Dennis, Saeed and Byron, I had started an all-nighter.
Here is what I got with a sunrise:

I can not deny that SOLID code has its price. It takes much more time (2x or maybe 3x to compare to writing a monolithic code).
Nevertheless, we get benefits such as extensibility and reusability.
Let’s say we want to run the same game in 3D space. We can easily make this modification with SOLID code.
The link to the problem https://leetcode.com/problems/divide-two-integers
The LeetCode page for this task can be found here
Link to the description of the task: https://leetcode.com/problems/longest-substring-without-repeating-characters/
Link to the description of the task: https://leetcode.com/problems/the-earliest-moment-when-everyone-become-friends/
Time Complexity Analysis:
List.Add(newFriend) -> O(1) if Count is less than Capacity, otherwise O(k) where k is Count
List.AddRange(anotherList) -> O(l) if Capacity is less than Count plus l, otherwise O(Count + l) where l is anotherList.Count
List.Contains(member) -> O(k) where k is Count
Loop:
The total complexity is m * O(n). Also, m must be equal or larger then log(n) to make all members connected. This way the solution complexity is at least O(log(n) * n)
Two problems with this method:
Time Complexity Analysis:
HashSet.Add(newFriend) -> O(1) if Count is less than Capacity, otherwise O(k) where k is Count
HashSet.UnionWith(anotherHashSet) -> O(l) if Capacity is less than Count plus l, otherwise O(Count + l) where l is anotherHashSet.Count
HashSet.Contains(member) -> O(1)
Loop:
The total complexity is m * O(l). It is possible to minimize l by comparing HashSet.Count and anotherHashSet.Count, and then adding smallest to the biggest.
This way the total complexity is about O(m * log(n)) which makes the answer acceptable.
Link to the description of the task: https://leetcode.com/problems/add-two-numbers/
Conclusion:
It looks pretty nice!
What do I think about events in C#? I think they are not so different from what we have in real life. And when we have an event, we need to think of three things: who is the host, who are the guests, and what do we need to put onto the invitation cards.
Continue reading “Events in C#: Let’s Party”
Recently, I ran into an issue involving implicit type conversion. Before this case, I expected that compiler took care of any implicit conversions it allowed. Apparently, it is not true.
Continue reading “C#: Even implicit conversions of types are not safe”When you set a reference type to ‘null’ like this:
string str = null;
it means that it’s undefined. It’s not a zero or empty. It’s nothing. I wonder what nothing looks like inside of computer memory.
Continue reading “C#: What ‘null’ looks like in computer memory?”